

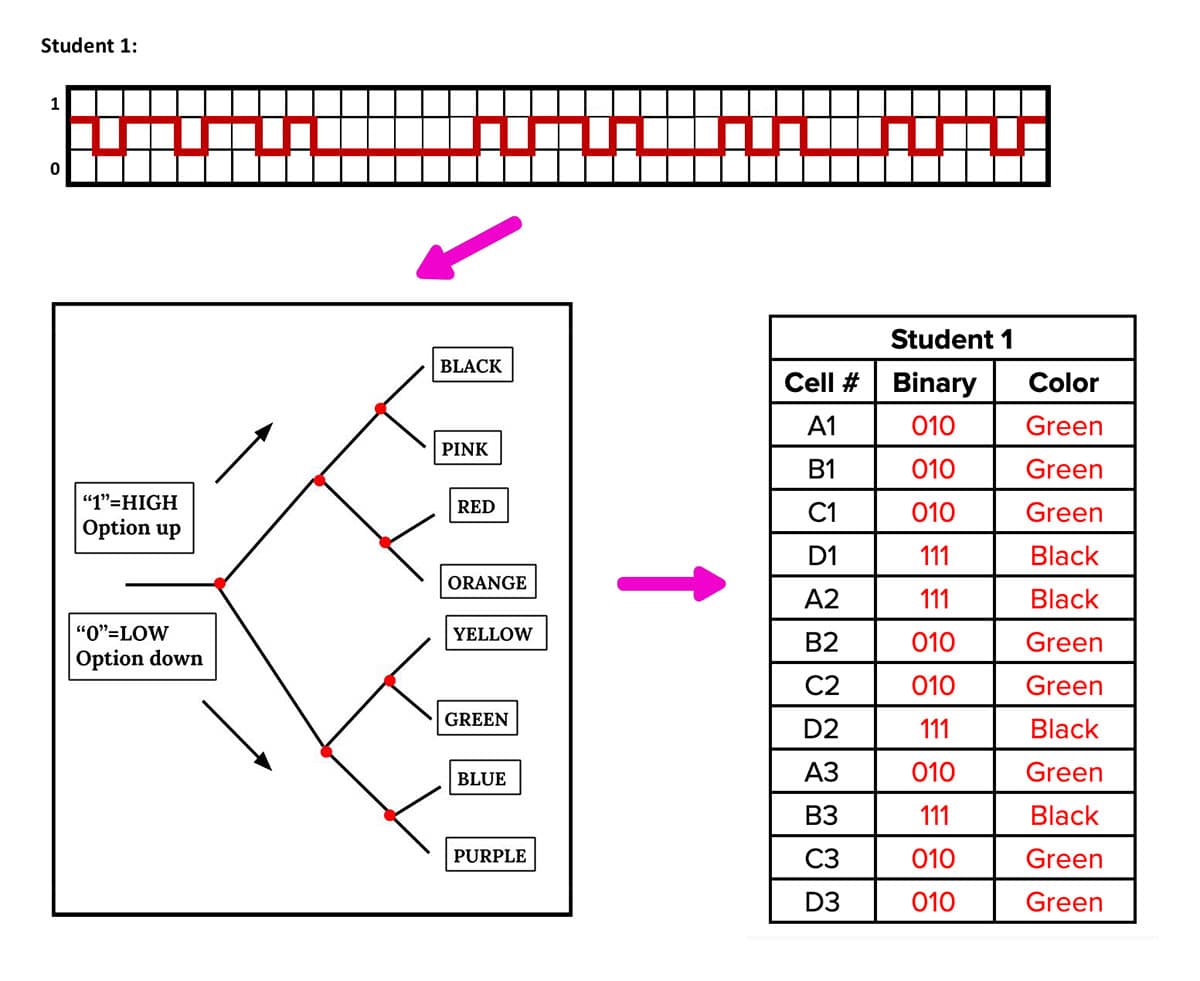
Computers don’t understand language or numbers in the same way that we do. The main reason the binary number system is used in computing is that it is simple. But, aside from needing more digits to express much smaller numbers (e.g., sixteen is described as 16 in the decimal system and 00010000 in binary), the concept is the same. Thus, binary numbers are usually organized in at least four digits or eight digits, depending on how big the number is. The binary system uses bits, twos, fours, eights, sixteens, and so on. Our regular counting system uses units, tens, hundreds, and thousands to represent the extra lines of digits. Therefore 0010 equals two (one lot of two and no bits), 0101 denotes five (one lot of four, no twos, and one bit), and so on. This is because, in a binary system, we can only count 0 and 1 before we run out of symbols and have to re-use them in the second line of digits. The base-2 numeral system works the same way but, instead of having ten different symbols available before another digit needs to be added, there are only two. Ten lots often are denoted as 100, and we call this number a hundred. For example, we can denote up to 99 (nine lots of ten and nine units) before we have to add another digit. Every extra digit we add in our base-10 counting system represents a multiple of tens. Twenty-one (21) written in numerals means two lots of ten and one units. In this way, the symbol for ten (10) means 1 lot often and no units. In our base-10 counting system, a single digit is called a unit. We can count from 0 through to 9 before we run out different symbols, and so, when we get to ten, we represent it by combining a 1 and a 0. This means that we have 10 different symbols, or numerals, available to represent different numbers. Instead, we use the base-10 - or decimal - numeral system. In our everyday life, we don’t count using a base-2 system. Every single digit is referred to as a bit. All numbers in a base-2 numeral system are denoted using one or the other of these symbols. A binary number is described using the base-2 numeral system, which uses only two different symbols, or numerals: usually 0 and 1. A binary choice, for example, involves picking one of two possible options. Decimal Numbersīinary means one or the other.

To understand how this is possible, it’s important first to understand the binary numbering system and its works. Thus, it is the basis for the storage and transfer of data in most digital electronic devices. In addition, the binary numbering system is used to code everything from memory to images on the screen. The binary numbering system is used in computing and electronics because it’s the simplest counting method available.


 0 kommentar(er)
0 kommentar(er)
